Cuando la trayectoria de una partícula en movimiento describe una curva cualquiera, estamos frente a un tipo de movimiento denominado curvilíneo. La velocidad de la partícula siempre es tangente a la trayectoria descrita, por lo que si "v" es la magnitud de la velocidad esta cambia en el tiempo, es decir " v=v(t) ", es una función del tiempo, y la dirección de la velocidad en cada punto de la trayectoria está dada por el vector unitario en la dirección de la velocidad.En cada punto del movimiento se asigna un sistema coordenado móvil, ejes normal y tangencial N y T respectivamente. a cada uno de estos ejes se asocia un vector unitario normal y tangencial para los ejes N y T respectivamente.
La Aceleración de la partícula en movimiento en cada punto de la trayectoria tiene dos componentes, una en la dirección normal apuntando hacia le centro de curvatura y otro en la dirección tangente.
La componente tangencial de la aceleración es la responsable del cambio en la magnitud de la aceleración mientras que la componente normal es la responsable del cambio de dirección de ña partícula en su recorrido.
La aceleración total es la suma vectorial de las aceleraciones normal y tangencial en todo instante del tiempo y esta apunta hacia la concavidad de la trayectoria.
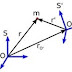
El centro de curvatura es instantáneo y se forma cuando los ejes normales para dos instantes del movimiento se cruzan, y la distancia desde le centro de curvatura hacia la posición de la partícula define lo que se conoce como el radio de curvatura.
Entonces la aceleración para cualquier instante del tiempo si a, aN, aT son vectores la aceleración total se escribe asi: a = aN + aT
La magnitud de la aceleración normal está dado por a N = v2/R, "v" es la magnitud de la velocidad, R el radio de curvatura y la magnitud de la aceleración tangencial está dada por a T = dv/dt, es decir la derivada de la función v=v(t) para cada punto de la trayectoria.
Siempre que estamos frente a un movimiento en trayectoria curvilínea no debemos olvidar que la aceleración actúa en las direcciones normal y tangencial.
Subscribirse a www.mjfisica.blogspot.com
Nenhum comentário:
Postar um comentário
Deja Tu Pregunta, Duda, Comentario Ahora: